Как научиться делить столбиком (уголком): примеры с решениями и объяснением

На чтение: 21 минРубрика: Подготовка к школе

Обучение делению с остатком

Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:

Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
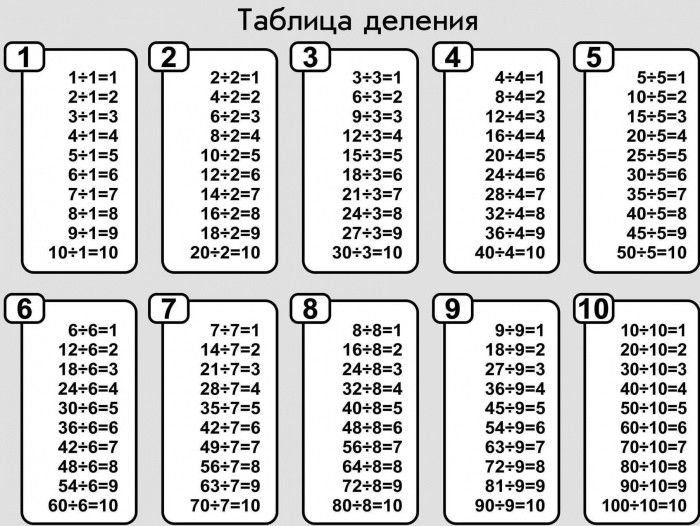
Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
Запишите под числом 35 число 32.
Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.

Простые примеры для ребенка

На этом же примере можно продолжить:

При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.

Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.

Обучение делению в столбик в тетради

Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.

Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.

Объяснять математическое действие нужно подробно:

Напишите в тетради пример: 105 разделить на 5.
Запишите это, как при делении в столбик.
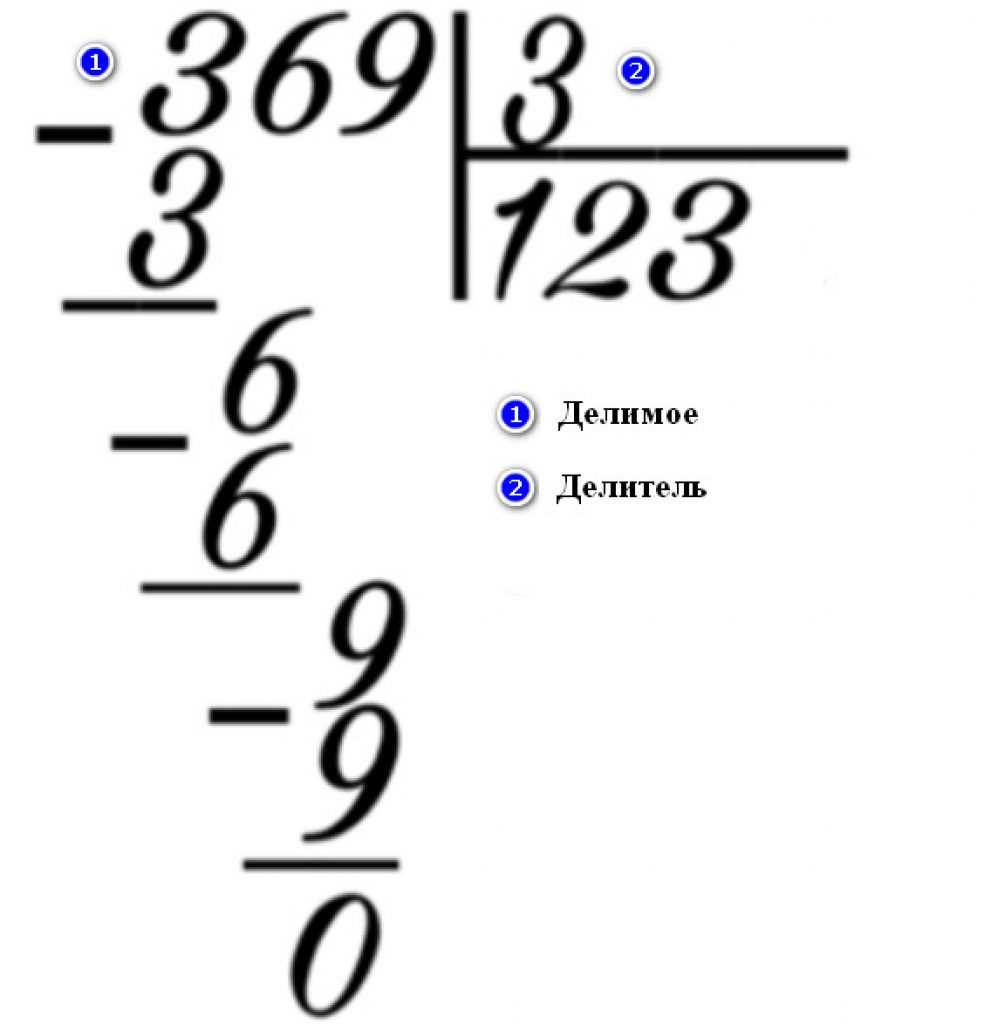
Расскажите, что 105 – делимое, а 5 – делитель.
С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
В столбике деления, под числом 5, напишите цифру 2.
Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.

Родителям нужно объяснить, что это деление не имеет остатка.

Начать деление можно с цифр 6,8,9,
затем переходить к 22, 44, 66
, а после к 232, 342, 345
, и так далее.

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

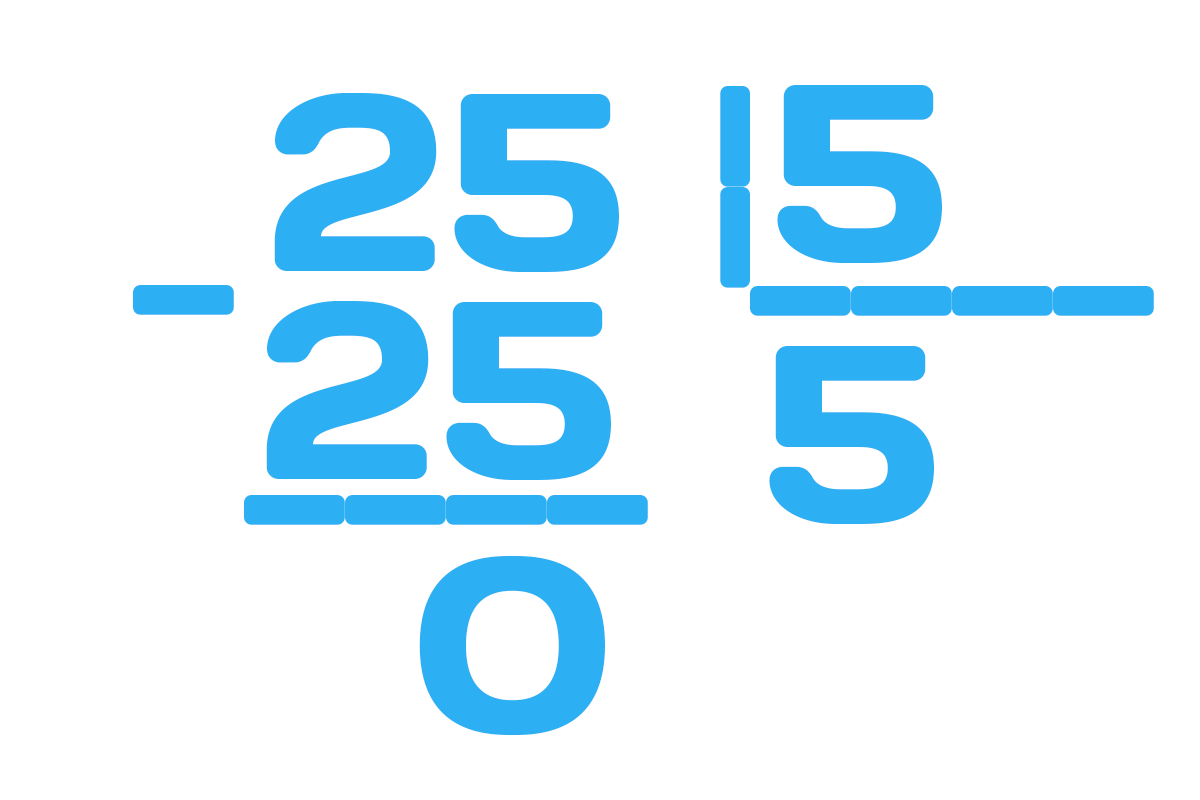
Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Деление сотен в столбик (чисел от 100 до 999)

Деление в столбик не зависит от количества цифр в делимом, отличается лишь количество необходимых операций, то есть чем больше цифр в делимом и меньше в делителе, тем больше будет этапов для нахождения частного (ответа или результата деления цифр).

Но также при делении чисел из 3 цифр существуют особенности, для примера возьмём 525 и разделим его на 25:

Шаг 1. Запишем пример для деления в столбик:

Шаг 2. Деление числа начинается слева направо, но так как у нас делитель состоит из 2 цифр (25), то можно сразу начинать проверку возможности деления первых 2 цифр, алгоритм поиска при делении в столбик всегда одинаков:

Если делимое состоит из 3 цифр а делитель из 2, то вначале всегда можно брать 2 первые цифры и искать первую цифру в частное.

Шаг 3. Из 52 необходимо вычесть полученный результат то есть 50, а цифру 2 необходимо зависать в частное.

Шаг 4. После вычитания полученную цифру (в примере 2) необходимо записать и к ней добавить цифру из делимого, получаем 25, с этим числом необходимо повторить расчёт:

Шаг 5. Записываем полученные цифры.

Ответ: 21.

Как выучить деление и умножение с ребенком

Самый элементарный метод, с помощью которого можно научиться умножать и делить, представлен наглядной демонстрацией разделения предметов на равные части или же увеличения этих долей. В роли предметов, которые используются в качестве обучающего реквизита, должны выступать предметы, вызывающие в уме школьника интерес.

Умножение и деление однозначных чисел

Для деления однозначных чисел на однозначные лучше всего использовать таблицу умножения, но перед этим следует объяснить своему чаду, что деление – это действие, противоположное умножению. Сделать это можно с помощью любого правильного деления натуральных чисел, к примеру, 2 умножить на 4 будет 8. Придерживаясь данного примера, показать карапузу делительный процесс:

разделить 8 на любой множитель, например, на число 2;
в ответе получится 4, то есть множитель, который не был использован при делении.

Таким методом также делятся многозначные (двухзначные) числа на однозначные. А для того, чтобы освоить процесс умножения однозначных чисел, вместе с малышом достаточно лишь постепенно учить таблицу умножения.

Алгоритм деления однозначных чисел

Умножение и деление двузначных чисел

В целях разъяснения дошкольнику процесса умножения двухзначных цифр опытные педагоги рекомендуют прибегать к итальянскому методу или методу «решетки». Для начала следует на листе бумаги начертить мини-таблицу два на два: одно число записать по длине, а другое – по ширине таблицы. Каждую клетку нужно разделить по диагонали ровной линией, после чего в образовавшиеся треугольники вписать результат умножения чисел (отдельно десятки, отдельно единицы).

Далее вместе с ребенком сложить «произведения» строго по диагонали, результат подписать. Произведение будет равно значению, которое образуется в процессе чтения цифр снизу вверх и направо.

Некоторые родители предпочитают использовать китайско-японский способ умножения в процессе обучения своих детей. Он может показаться более сложным, чем метод «решетки», но на деле все не так страшно. Следует всего лишь нарисовать цифры линиями, посчитать «узлы», которые образовались при пересечении, и «собрать» из них произведение. В процессе подсчета учитываются следующие моменты:

количество узлов, которые получились при пересечении линий, обозначающих десятки перемножаемых чисел = количество сотне произведения;
узлы, получившиеся при пересечении прямых, обозначающих единицы и десятки умножаемых цифр = количество десятков произведения.

Обратите внимание! Что касается количества узлов, образовавшихся путем пересечения линий, которые обозначают единицы умножаемых чисел, то оно равняется количеству единиц произведения. Если ребенок еще не проходил метод деления двухзначных цифр «столбиком», то нужно объяснить ему на более простом языке

Для примера можно взять 66/3. Число 64 раскладываем на цифры, которые устно можно поделить на 3:

Если ребенок еще не проходил метод деления двухзначных цифр «столбиком», то нужно объяснить ему на более простом языке. Для примера можно взять 66/3. Число 64 раскладываем на цифры, которые устно можно поделить на 3:

64 = 30 + 30 + 6.

Малышу сразу все станет понятно: 30 и 6 мы сможем поделить на 3, после чего нужно будет только сложить результаты, т. е. 66 / 3 = 10 (получили в процессе деления 30 на 3) + 10 (30 поделили на 3) + 2 (6 поделили на 3).

66 / 3 = 22. Здесь не был использован метод разделения в столбик, но карапуз сразу поймет ход рассуждений и выполнит простые вычисления без труда.

Умножаем и делим, используя таблицу умножения

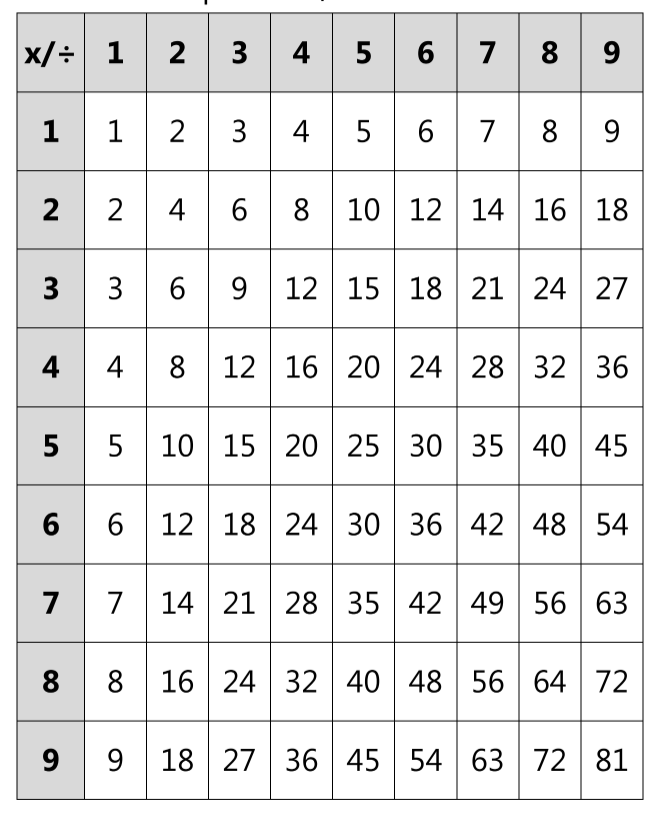
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.

Пример:
4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.

Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.

Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг
. Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг
. Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг
. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг
. Ставим точку под делителем.

5 шаг
. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг
. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг
. Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг
. Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг
*. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг
Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)
(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Принцип деления для детей

Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.

Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.

Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.

Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.

После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.

Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.

Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку»

Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик

Наглядный пример для ученика и родителей

Деление в столбик можно наглядно объяснить на этом примере.

Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.

Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.

Для того чтобы в школе у ребенка не было проблем с уроками, необходимо давать ему базовые знания с самого раннего возраста. Ведь намного проще объяснить ему некоторые вещи в процессе игры, а не во время строгого школьного урока.

Принцип деления для детей

Ребенок часто сталкивается со многими математическими понятиями, даже не догадываясь о них. Ведь все мамы, играя с малышом, рассказывают о том, что у папы супа налито больше, к бабушке идти дольше, чем до магазина и прочие простые примеры. Все это дает малышу начальное представление о математике.

Стоит попробовать предложить ребенку поиграть в игры с делением. Поделите яблоки (груши, вишни, конфеты) между мамой и ребенком, постепенно добавляя и других участников: папу, игрушку, кошку. В начале малыш будет делить, раздавая всем по одному предмету. А вы потом подведите итог. Скажите ему, что было всего 6 яблок, вы разделили их на троих человек, и каждому досталось по два. Объясните, что слово разделить – это значит раздать всем поровну.

Если вам нужно объяснить деление с цифрами, то также можно привести игровой пример. Скажите, что цифры – это те же яблоки. Расскажите, что то число яблок, которое нужно разделить – это делимое. А то число человек, на которых нужно поделить эти яблоки – это делитель. Покажите несколько примеров наглядно. В игровой форме ребенок обязательно все поймет.

Как научить ребенка делению столбиком?

Если вы учите ребенка делить столбиком, то, скорее всего сложение, вычитание и умножение в столбик он уже освоил. Если нет, то обязательно подтяните эти знания, иначе, добавив еще и деление, ребенок вообще запутается.

Итак, делим в столбик. Возьмем не сложный пример: 110 нужно поделить на 5.

Запишем делимое — 110, а рядом с ним делитель – 5.
Разделим все это уголком.
Начинаем объяснять, вот пример диалога:

-Первая цифра 1. 1 на 5 делится?

-Нет.

-Значит, берем следующую самую маленькую возможную цифру, которая делится на 5 – это 11. Сколько раз цифра 5 может поместиться в 11?

-Два раза.

— Записываем цифру 2 в уголке под пятеркой. Проверяем, умножаем 5 на 2.

— Получается 10.

— Записываем это число под 11. Делаем вычитание. 11 минус 10?

— Равно 1.

— Пишем 1 и рядом сносим 0 из делимого (110 которое). Получилось 10. 10 на 5 делится?

— Да, получается 2.

— Записываем 2 под 5.

Для того чтобы облегчить изучение деления, сейчас появились таблицы деления для детей. Принцип действия у них тот же, что и у таблицы умножения. Вот только надо ли учить таблицу деления, если уже выучил умножение? Это будет зависеть от школы и преподавателя.

просмотров

Принцип деления для малышей

Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.

Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.

Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.

Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.

Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.

Как делить столбиком

Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:

В нашем случае число 78 будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше

К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

780 : 12 = 65.

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.

Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:

9027 : 9 = 1003.

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.

Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:

Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:

3000 : 6 = 500.

Обучение делению в столбик в форме игры

Можно поставить задачи таким образом:

1Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.

2Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.

3Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.

4Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.

Деление чисел

Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.

Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.

Рейтинг

( Пока оценок нет )

Editor/ автор статьи

Давно интересуюсь темой. Мне нравится писать о том, в чём разбираюсь.

Добавить комментарий

Секрет опытного учителя: как объяснить ребенку деление в столбик

На чтение: 20 минРубрика: Советы

Как проводится

Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.

Приведем простой пример того, как делить с остатком:

Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:

5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.

Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.

Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.

Основные этапы:

Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 помещается, 5*2=10 помещается, 5*3=15 помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.

Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя

Как научить считать в пределах 20

Педагоги, родители подают рекомендации, предлагают проверенные алгоритмы, благодаря которым маленький ученик постигнет, что такое десятки, как усвоить более сложные понятия. Всегда испытывайте, запомнил ли «юный математик» пройденный материал, не перескакивайте, даже если на изучение удалится не 2–3 дня, а неделя.

С чего приступить

Алгоритм:

выучите названия чисел второго десятка;
понадобится два комплекта кубиков. Предметы должны быть одинаковые;
ребёнок должен выложить в ряд 10 предметов, обязательно слева направо;
скажите, что 10 – это десяток, он называется «дцать»;
на первоначальный ряд кубиков положите ещё один. Получилось – 11 или один плюс «дцать» = одиннадцать;
возложите два, затем три, четыре кубика на «дцать». Получилось: три – на – дцать, четыр – на – дцать и так дальше;
пусть маленький ученик сам ставит кубики, прибавляет знакомую цифру к десятку;
дитя чётко запомнил схему построения чисел от 11 до 19? Переходите к вытекающему этапу.

Как образуется сотня

Алгоритм:

большинство деток, хорошо освоивших образование чисел до 20, быстро понимают, как сделать два, три, четыре десятка до сотни;
начин упражнения то же: выложите 10 кубиков, скажите, что это десяток или «дцать»;
рядышком поставьте такой же ряд из десяти кубиков, получилось два ряда. Название: два плюс «дцать» = двадцать, три плюс «дцать» = тридцать;
40 (сорок) и 90 (девяносто) покиньте на потом, скажите: у этих круглых чисел другое название. Покажите, что у десятка вечно «0» на конце, потому число круглое, к нему прибавляются цифры 1, 5, 8 и так дальше;
50, 60, 70, 80 – ещё проще запомнить. Спросите, сколько десятков в числе 50. Верно, пять. Пусть детки назовут первую цифру, прибавят слово «десят» – выйдет ПЯТЬДЕСЯТ. Когда ученик понял принцип, спросите: «Сколько десятков ты отыскал в 60, 70 и 80?» Конечно, шесть, семь, восемь. Так получатся новоиспеченные названия: ШЕСТЬДЕСЯТ, СЕМЬДЕСЯТ, ВОСЕМЬДЕСЯТ.

Счёт до 20 без перехода сквозь десяток

Алгоритм:

вновь достаньте те же кубики;
пусть ребёнок выстроит ряд из десяти штук;
поставьте сверху (обязательно слева направо) ещё два кубика. Вышло 12;
рядом по тому же принципу постройте число 15;
объясните маленькому ученику, как скоро сложить 12 и 15. Прибавьте 1 + 1 десяток, получилось 2 десятка или ДВАДЦАТЬ;
добавьте единицы: 2 + 5 = 7. Теперь есть ДВАДЦАТЬ и СЕМЬ, вместе – ДВАДЦАТЬ СЕМЬ;
подкрепите объяснение кубиками. Пускай ребёнок пересчитает, действительно ли 27 кубиков на столе;
закрепите задание, дайте попробовать разные варианты, пока «юный математик» не постигнет принцип;
сложение освоено? Приступайте к вычитанию: принцип тот же;
через десяток переходите лишь после полного понимания материала с любыми числами от 10 до 100.

Рекомендация! К началу обучения ребёнок должен чётко понимать, где десятки, а где – колы в двузначном числе, чётко знать понятия «лево – право».

Правила счёта с переходом сквозь десяток

Используйте таблицу, в которой показан состав числа. Детки должны соображать, как получить цифры разными способами. Например, 8 = 3 + 5, 4 + 4, 6 + 2, 7 + 1, 8+ 0. Без навыков скорого счёта, сложения/вычитания от 0 до 10 нельзя переходить к более сложным упражнениям.

Задача родителей: разъяснить, что одно из чисел нужно разложить на два, чтобы получить 10, затем добавить остаток. Правило легко понять на примере.

Смотрите:

задача: отыскать, сколько будет 18 + 6;
18 – это 10 и 8;
запишите по-новому (10 + + 6;
спросите, сколько от 6 не хватает до десятка, чтобы добавить к 8;
правильно, 2 (пригодится таблица «Состав числа);
теперь запишите 6 как 2 и 4. Вышло: 10 + 8 + 2 + 4 или 10 + 10 + 4. Два десятка плюс четыре единицы равно ДВАДЦАТЬ ЧЕТЫРЕ;
когда дитя запомнит сложение, так же объясните вычитание;
всегда держите под рукой таблицу «Состав числа». Детки будут меньше теряться, несложнее ориентироваться.

Постоянно проводите «тренировку между делом», чтоб лучше запомнился состав числа. Проговаривайте пуще, подключайте ребёнка, пусть оканчивает фразу: «На столе слева стоит 3 тарелки, я устанавливаю справа ещё 3 тарелки. Сколько всего предметов? Правильно, 6». Покажите иной способ: «Я поставлю слева 2 тарелки, справа – 4 тарелки, вновь вышло 6 тарелок» и так далее (1 + 5).

Что нужно для освоения деления в младшем школьном возрасте

Деление — это не первое арифметическое действие, которое осваивают дети. Поэтому, прежде чем браться за «делимое-делитель-частное», нужно обязательно выяснить, знает ли ребёнок разряды чисел и понимает ли принципы:

Таблицей деления дети могут проверять решения примеров

Эффективные способы объяснения деления школьникам

Все способы объяснения можно условно поделить на академичные и образные. Первые опираются на цифры, то есть записываются в виде арифметических примеров, вторые — на конкретные предметы: конфеты, мячи и т. д., которые умозрительно делятся между людьми, игрушками.

В работе с учениками начальной школы эффективным будет синтетический способ, совмещающий опору на образы и цифры одновременно.

Деление на основе знания таблицы умножения

Для понимания сути деления стоит обратиться к вычислениям с опорой на таблицу умножения.

Записываем пример: 2 х 5 = 10.
Берём 10 монет и просим поделить их на двоих — получается две стопки по 5 монет.
Далее 10 монет делим на пятерых — получается 5 стопок по 2 монеты.
Вывод — при делении мы выясняем, сколько раз каждый множитель помещается в произведении.

На этом приёме разъясняем понятийную базу: то число, которое делится, называется делимое, то число, на которое делится — делителем, а результат — частным.

Поскольку деление обратно умножению, то второе может проверить результат первого.

Первое время для закрепления навыка можно зарисовывать схему перестановки значений при делении и при проверки умножением

Делимое делим на делитель, то есть 10 : 2.
Получаем частное — 5.
Проверяем умножением, то есть частное умножаем на делитель — 5 х 2.
Получаем 10, что в исходном примере является делимым.

Деление двузначных чисел на однозначные

Чтобы разделить двузначное число, не являющееся произведением таблицы умножения, на однозначное, нужно каждую цифру делимого разделить на делитель и записать первое частное десятками, а второе — единицами. Например, 86 : 2.

Делим 8 на 2. Получаем 4.
Делим 6 на 2. Получаем 3.
Ответ — 43.
Проверяем — 43 х 2 = 86.

Деление способом группирования

Суть этого способа деления заключается в подсчёте количества групп равных делителю, которые помещаются в делимое. Результат будет частным.

Задача состоит в распределении мячей между командами. Решаем пример — 30 : 3.

Группирование предполагает использование наглядных материалов

Как объяснить деление в столбик

Поскольку деление может быть без остатка, а может быть с остатком, рассмотрим два варианта объяснение такого арифметического действия.

Деление без остатка

Решим пример 396 : 3.

Выполняя деление в столбик, ребёнок должен правильно оформить запись, чтобы значения «не съехали» с нужных позиций

Деление с остатком

Решим пример 90 : 4.

Важно обратить внимание ребёнка на то, что перед добавлением нуля к остатку в столбике, нужно поставить десятичную запятую в частном

Деление на двузначные числа

Если в делителе есть десятки, сотни, то для облегчения решения делитель можно упростить, разбив на единицы (десятки).

Для деления на десятки нужно воспользоваться правилом упрощения

Решим пример — 405 : 15.
Разобьём 15 на единицы, на 5 и 3 — их произведение равно 15.
Теперь решаем два примера. Сначала 405 : 5. Частное 81.
Затем 81 : 3. Частное 27.
Результат — 405 : 15 = 27.

Видео: тренажёр быстрого деления в уме для школьников

Объяснить деление можно не только школьнику, но и дошкольнику. Причём не только в условиях детского сада, школы, но и дома. Для этого нужно убедиться, что ребёнок имеет опорные знания, и у родителя есть запас времени, терпения для регулярных занятий со своим чадом.

Источник

Обучение делению в столбик в форме игры

Можно поставить задачи таким образом:

1
Организуйте ребенку место для обучения в форме игры.
Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.

2
Обучать математическому действию можно с помощью цифр.
Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.

3
Дайте ребенку 6 груш.
Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.

4
Расскажите ученику о делении с остатком.
Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.

Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел.
Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.

Обучение делению в столбик при помощи таблицы умножения

Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:

Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.

Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.

Таблица умножения

Счет до 20

сказать, что каждое следующее число состоит из двух цифр;
первая цифра – это десятки, а вторая – единицы, которые идут по порядку от 1 до 9, как в счете до 10;
обязательно используем наглядность;
почаще тренируйтесь: заведите большое количество маленьких мячиков, игрушек или используйте конфеты и фрукты. Просите малыша достать из одной коробки, например, 15 мячиков и переложить их в другую. Рисуйте и лепите цифры, играйте с магнитными, пусть они ходят к друг другу в гости и составляют двузначные числа друг из друга;
просите малыша называть цифры-соседи: «Кто живет по соседству с числом 17?»;
учите распознавать геометрические фигуры;
учите распознавать понятия «длинный-короткий», «высокий-низкий», «большой-маленький», «тяжелый-легкий», «один-много», «много-мало» и т.д., постоянно комментируя и сравнивая друг с другом предметы, которые вас окружают;
учите распознавать понятия «право-лево», «вперед-назад», постоянно комментируя свои движения и направления действий.

Правила деления в столбик

Деление в столбик позволяет разделить любое число без использования калькулятора или иных средств, которые автоматически показывают результат.

Для деления в столбик потребуется только листок и ручка (карандаш), в отличие от обычного деления, деление в столбик имеет свои особенности:

Особую запись примера, при делении в столбик решение записывается не строку, а в столбик.
При делении в столбик может остаться «остаток» — число которое нельзя разделить, например, при делении 10 на 4 остаток будет 2, таким образом, ответ будет: 10/4=2 (остаток 2), при нормальном делении 10 на 4 результат будет 2,5.
Нельзя проводит операции с дробями, при делении в столбик можно делить только целые числа, то есть число 2,4 (две целы четыре десятых) разделить не получится.

Как выучить таблицу сложения и вычитания в пределах десяти?

После того как ребенок знает порядок числительных, полезно применять задания на состав числа. Можно, конечно, зазубрить состав числа 5, например, но лучше использовать игровые действия с предметами с параллельной установкой на запоминание.

Например:

В одной тарелке было 4 апельсина, а в другой — 2. Сколько всего апельсинов? (Задача на нахождение суммы)

Всего 6 яблок, а друзей — трое. Разделите каждому поровну, одинаково.

Сочетать с простыми задачами можно и маленькие схемы, которые легко применять на уроке и дома.

На переместительный закон сложения не сложно привести такой пример: одна тарелка с двумя яблоками лежит на столе, а другая тарелка с четырьмя яблоками — лежит рядышком, если поменять их местами, то все равно общее количество яблок останется неизменным.

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль : 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4 · 0 = 0 14 ; 4 · 1 = 4 14 ; 4 · 2 = 8 14 ; 4 · 3 = 12 14 ; 4 · 4 = 16 > 14 .

Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .

3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.

4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .

Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .

Принимаем это число за рабочее и снова выполняем пункты алгоритма.

2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.

4 · 0 = 0 2 ; 4 · 1 = 4 > 2

Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .

3. Выполняем операцию вычитания и под чертой записываем результат.

4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.

Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:

В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9 .

После второго, третьего и четвертого шага алгоритма запись примет вид:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7 .

Как выучить деление и умножение с ребенком

Умножение и деление однозначных чисел

разделить 8 на любой множитель, например, на число 2;
в ответе получится 4, то есть множитель, который не был использован при делении.

Алгоритм деления однозначных чисел

Умножение и деление двузначных чисел

количество узлов, которые получились при пересечении линий, обозначающих десятки перемножаемых чисел = количество сотне произведения;
узлы, получившиеся при пересечении прямых, обозначающих единицы и десятки умножаемых цифр = количество десятков произведения.

Для примера можно взять 66/3. Число 64 раскладываем на цифры, которые устно можно поделить на 3:

64 = 30 + 30 + 6.

Как делить столбиком числа с нулями?

Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.

Из нюансов отметим:

при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.

Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.

Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.

Практикуйте полученные знания и помогайте своему чаду осваивать математику.

Поскольку операция деления простых чисел является одним из важных математических действий, многие родители задумываются о том, как научить ребенка делению. Перед тем, как приступить к обучению, вы должны убедиться в том, что малыш уже умеет вычитать, складывать и умножать числа. Лучше всего приступать к изучению деления столбиком, когда ребенок отправляется в третий класс

Очень важно объяснить, что деление представляет собой процесс, по ходу которого целое разбивают на отдельные части. Не забудьте учесть знания таблицы умножения – убедитесь в том, что кроха уверенно знает ее

Перед тем, как серьезно приступить к обучению, попробуйте освоить эту нехитрую науку в игровой форме. Для того чтобы сформировать у малыша представление о том, что деление – это разбор целого на части, дайте ему несколько предметов и попросите разделить между членами семьи или игрушками. При этом эффективно использовать нечто целое – фрукт или овощ, например, который можно разрезать на кусочки.

Потренируйтесь на кубиках. Возьмите парное количество этих элементов и предложите ребенку разделить их поровну между собой и вами. Варьируйте задание. Добавьте такое количество кубиков, чтобы их общее количество делилось на три или шесть. Затем можно усложнить задачу и делить на восемь, семь или девять. После выполнения каждого задания тщательно анализируйте результат вместе с малышом. Он должен понимать сам процесс. Если что-то ему непонятно, постарайтесь доходчиво это объяснить. Не зацикливайтесь на определенных предметах. Постоянно меняйте их, чтобы ребенок приспосабливался делить любые объекты.

Важно! Для начала составляйте задания таким образом, чтобы малыш проводил действия с четным количеством объектов. Таким образом, у ребенка получится одинаковое количество предметов

Это пригодится на следующем этапе, чтобы дать понять малышу, что деление – операция обратная умножению.

Вместе с этим ищут и читают:

Рейтинг

( Пока оценок нет )

Editor/ автор статьи

Давно интересуюсь темой. Мне нравится писать о том, в чём разбираюсь.

Добавить комментарий